Neoneuron

Neoneuron represents the practical validation of my Ph.D. Thesis: a novel generic methodology for high-performance geometry generation.

The core research addresses a universal challenge in computer graphics: generating high-fidelity meshes from compact representations without exhausting GPU memory. I developed a pipeline based on Mesh Shaders capable of constructing any complex, branching topology entirely on the GPU, bypassing the limitations of traditional pre-computed meshes.

To stress-test this general-purpose architecture, I developed Neoneuron as a demanding use case. Neuronal morphologies, with their intricate, recursive branching and massive scale, serve as the ultimate benchmark to demonstrate that this procedural approach offers superior scalability and flexibility compared to standard rendering techniques.

The Core Innovation: The Schemlet

The central contribution of this research is the Schemlet. Unlike a meshlet (which stores geometry), a Schemlet is a blueprint. It is a lightweight, symbolic instruction packet that tells the GPU how to build a part of the neuron.

Scientific Methodology

The methodology redefines the rendering pipeline, replacing the traditional Input Assembler with a compute-driven architecture tailored for biological structures. The process is divided into three distinct stages:

1. Ingestion & Decomposition (CPU)

The CPU’s role is minimized to a one-time preprocessing step. It ingests the raw neuronal skeleton and decomposes the hierarchical tree into a flat, cache-friendly array of Schemlets.

• Geometric Pre-calculation: Critical static data is computed offline. For segments, a modified Ramer-Douglas-Peucker algorithm assigns an importance value to each control point for efficient LOD culling.
• Topological Solving: For bifurcations, optimal division angles are pre-solved to ensure seamless branching angles before the data ever reaches the GPU.

2. Task Shader Evaluation (GPU)

Before any vertex is processed, Task Shaders act as a high-performance dynamic filter. Each workgroup evaluates a batch of Schemlets in a two-phase process:

• Universal Culling: A bounding box is dynamically computed for each Schemlet and tested against the camera frustum. Invisible sections are discarded instantly, saving rasterization power.
• Adaptive LOD Calculation: For visible schemlets, a continuous Level of Detail factor is calculated based on screen-space metrics. This determines the exact vertex density (e.g., from 4 to 16 radial vertices) required for the next stage.

3. Mesh Shader Synthesis (GPU)

This is where the symbolic Schemlet expands into explicit geometry. The Mesh Shader employs a collaborative workflow where threads share calculated data via Workgroup Shared Memory to avoid redundant VRAM accesses.

• The Bifurcation Solver: One of the hardest challenges is creating watertight joints. The Bifurcation logic matches the vertex density of the parent and child segments dynamically, generating a procedural “patch” that sutures the three tubes together without cracks.
• Soma Deformation: The cell body is generated as a tessellated sphere. A deformation algorithm is applied in real-time, where the sphere’s vertices are weighted and pulled towards the neurite connection points, simulating an organic membrane structure.

> IMG_000

> IMG_001

> IMG_002

Research Results

The methodology was validated through a demanding neuroscience use case involving the real-time generation of detailed neuronal morphologies. We conducted extensive benchmarks comparing Neoneuron against state-of-the-art tools like NeuroTessMesh and Neuronize.

1. Memory Efficiency (VRAM)

The most critical bottleneck in scientific visualization is memory. Traditional methods requiring explicit geometry storage quickly saturate VRAM.

By using Schemlets, Neoneuron eliminates the need to store pre-generated meshes. The benchmarks demonstrate a drastic reduction in memory footprint:

• 6.3x more efficient than NeuroTessMesh (Tessellation-based).
• 38.5x more efficient than Neuronize (Physics-based generation).

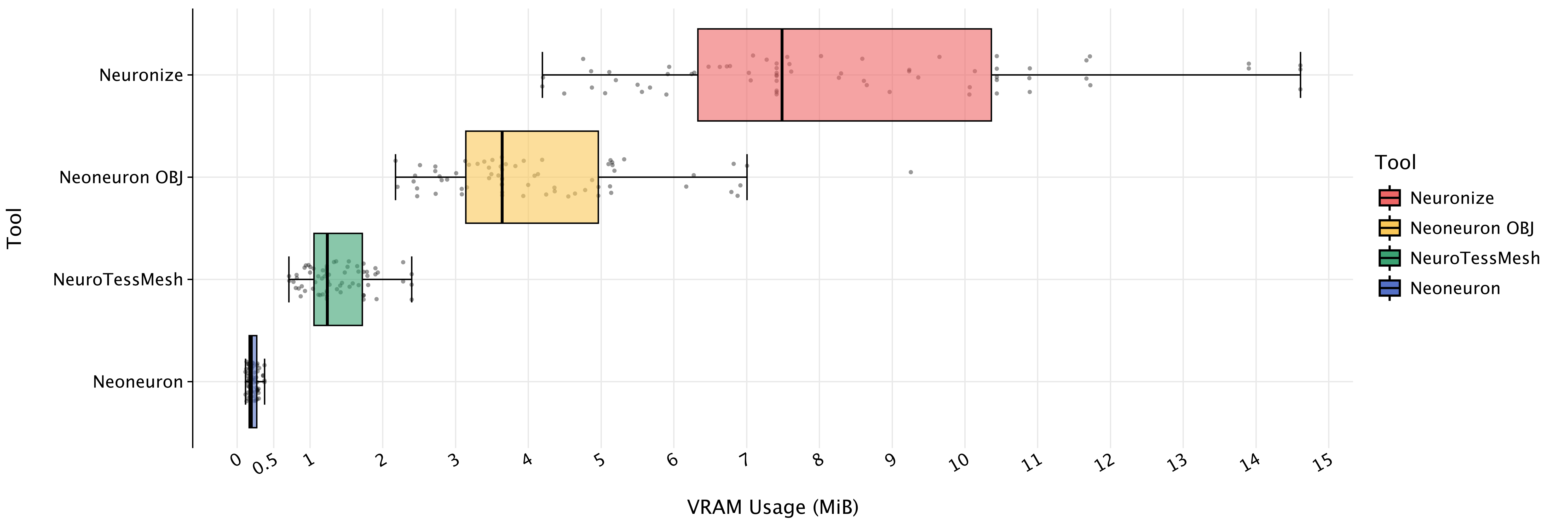
As shown in the distribution analysis, Neoneuron not only achieves the lowest mean memory usage (< 0.5 MiB per neuron) but also exhibits significantly less dispersion, ensuring predictable performance in large-scale scenes.

2. Rendering Performance

We measured the rendering throughput in frames per second (FPS) rendering identical complex scenes across different tools.

Despite the heavy computational load of generating geometry every frame, Neoneuron achieves an average FPS more than 2x higher than NeuroTessMesh. This performance leap is attributed to the GPU-driven pipeline, which saturates the GPU’s computational resources while eliminating the CPU-to-GPU bandwidth bottleneck common in hybrid approaches.

NeuroTessMesh

~20 FPS

High CPU overhead

Neoneuron

~45 FPS

GPU-saturated

3. Morphological Flexibility

Beyond raw performance, the system enables capabilities previously impossible in real-time. Since geometry is generated frame-by-frame, morphological parameters (soma radius, neurite thickness, bifurcation angles) can be modified instantly.

This contrasts with pre-stored geometry techniques, where such changes would require a complete regeneration and re-upload of the mesh buffers, causing significant stalls.

Challenges & Contributions

Publication Status

The paper describing this methodology is currently Under Review for publication in IEEE Transactions on Visualization and Computer Graphics (TVCG).

The thesis deposit is pending the final acceptance of this manuscript.